How to measuring equilibrium surface tension

 Michael Mulqueen and Paul D. T. Huibers

Massachusetts Institute of Technology, Cambridge, MA, USA

1 INTRODUCTION

The measurement of equilibrium surface tension is one of the oldest experimental techniques in the study of surfaces. Many of the techniques that are still in use today were originally developed in the 19th century. Significant improvements in accuracy and precision have been made over time, most recently as a result of the use of modern electronics and computers. This chapter briefly summarizes and discusses the advantages and disadvantages of the many experimental techniques that are in use today.

There is significant overlap in describing techniques for the measurement of equilibrium surface tension with those for dynamic surface tension, as discussed in the following chapter. Many of those dynamic surface tension methods can be used to measure equilibrium tension simply by performing the experiment over sufficiently long times. The time required for equilibration can range widely, from the practically instantaneous equilibration for pure liquids, to many hours or even days for dilute surfactant or polymer solutions. Thus, some of the dynamic techniques, particularly those that can only be used to study short times, such as the oscillating jet method, are not well suited for equilibrium measurements.

The surface tension measurement techniques can be divided into the following three categories: (i) Force Methods, which include the truly static methods of the capillary rise and Wilhelmy plate methods, as well as the dynamic detachment methods of the Du Noiiy ring and drop weight, (ii) Shape Methods, which include the pendant or sessile drop or bubble, as well as the spinning drop methods, and (iii) Pressure Methods, which are represented by the maximum bubble pressure method. These techniques are summarized in the following sections of this chapter.

1.1 Limitations

One key difference among the techniques covered in this review is that some involve processes that are not truly static, i.e. the interfacial area is changing as the critical measurement is made. For example, in the drop weight or the maximum bubble pressure method, the size of the drop or bubble, and therefore the interfacial area, is continuously increasing. If the rate of change is sufficiently small, the measurement will approach that of the equilibrium condition. This is often difficult to achieve and verify, particularly for dilute solutions of highly surface-active materials, which may take a long time (hours or even days) to reach equilibrium. With a truly static method, such as the capillary rise or Wilhelmy plate methods, one could allow the experiment to run for an indefinite amount of time in order to assure that equilibrium has been reached. For such cases, caution must be taken to ensure

that evaporation of the liquid is not significant. For solutions that take a very long time to equilibrate, or for measurements at elevated temperatures near the boiling point of the liquid, the pendant or sessile bubble methods are preferred as the vapor phase is small and inherently contained. This distinction does not necessarily segregate techniques into those suited only for equilibrium surface tension measurements and those suited only for dynamic measurements, since just as dynamic methods can be used to measure the equilibrium surface tension, static methods can be used to measure the dynamic surface tension.

One should also note that techniques which require a relatively small amount of the solution of interest, which is listed as an advantage in the descriptions that follow, may pose a problem for dilute solutions of highly surface-active materials. In these cases, the adsorption of the solute at the interface may significantly lower its concentration in the bulk solution. Theoretically, one could account for this by applying the following correction:

Where С and С are the corrected and uncorrected concentrations, respectively, A is the area of the interface, V is the volume of the solution, and Г is the amount of solute adsorbed at the interface per unit area, which can be obtained from surface tension measurements through the use of the Gibbs adsorption equation. However, there may also be a loss of material due to adsorption on to the solid walls of the vessel containing the solution which is difficult to quantify. Therefore it is typically desirable to keep гA /CV ≤1 and thus avoid the need for such corrections.

The precision for all of the techniques discussed below can be very good; typically, uncertainties between 0.1 and 0.01 dyne/cm are reported, provided the appropriate correction factors are used. However, one should note that for surface or interfacial tension measurements of dilute solutions of highly surface-active materials, such as surfactants, surface-active polymers or surface active biological materials, the presence of unknown and undesirable surface-active impurities can have a significant impact on the measured surface tension. The error introduced by these impurities is often much larger than the precision of the experimental technique.

2 CAPILLARY RISE

One of the oldest and simplest methods of measuring surface tensions is the capillary rise technique. This method utilizes the fact that when a tube is dipped into a liquid, surface tension (γ) forces cause the liquid to rise into the tube, as shown in Figure 11.1. In the less common case where the liquid does not wet the walls of the tubes, that is, the contact angle is greater than 90°, the liquid level will fall in the tube but the subsequent analysis remains the same. The liquid rises in the tube, pulled by a force in the vertical direction, given by (2πr) γcosθ, where r is the radius of the tube and θ　is the contact angle. At equilibrium, this force will be balanced by the weight of the liquid in the tube, which to a first approximation is given by (πr ²)hΔρg, where h is the height of capillary rise (measured from the minimum of the meniscus - see the following paragraph), （Δρ= ρ₁—ρ₂） is the difference in density of the bottom fluid (liquid 1) and the top fluid (liquid 2 or vapour), and g is the gravitational constant. Note that in the liquid-vapour case, ρ₁≥ρ₂and thus Δρ= ρ₁. This yields the following expression for the surface tension:

It is important to note that with all else being equal, a smaller tube radius (r) will give a larger and more accurately measurable capillary rise (h). In addition, as will be discussed below, the ideal limit given by equation (11.2) is approached only when r/h ≤ 1, so again a thin capillary tube is needed. Furthermore, the contact angle is usually difficult to measure; however, glass, provided it is thoroughly cleaned, is fully wetted (θ= 0) by most aqueous solutions. Glass also has the advantage of being transparent so that h is easily measured. To accurately measure the capillary rise, one need a relatively large vessel holding the liquid into which the capillary tube is placed so that the meniscus formed in the vessel does not interfere with the height measurement (see Figure 11.1). Therefore, a relatively large amount of liquid is required by this method.

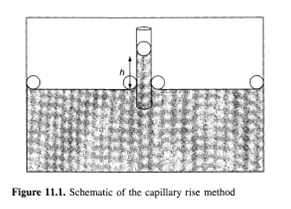
Since this is a very old and well-understood technique, a number of corrections to the ideal limit given in equation (11.2) have been proposed. These arise from the fact that this equation is derived by only accounting for the weight of the fluid below the apex of the meniscus. However, in theory the weight of the fluid in the meniscus (the shaded region in Figure 11.1) should also be included. The first and possibly easiest correction to implement is the polynomial expansion proposed by Lord Rayleigh (1) in 1915, given as follows:

By measuring h when r and Δρ are known, one can solve equation (11.3) by using numerical techniques to arrive at a more accurate value of у. Note that equation (11.2) is recovered as r/h becomes vanishingly small, and all but the first terms in the left-hand side are negligible. The second term of the series in equation (11.3) provides a correction for the weight of the fluid in the meniscus, assuming it is spherical, and the subsequent terms provide corrections (obtained by solving the Young-Laplace equation in differential form) to the spherical geometry assumption. Even more accurate corrections can be obtained by a more exact solution to the Young-Laplace equation. For example, Lane (2) provides an iterative method for obtaining a corrected surface tension. A more exact numerical solution of the Young-Laplace equation can now be obtained by advanced computational techniques to determine the meniscus profile (see Section 6 below for more details), leading to an even more precise correction to the measured surface tension.

In summary, the advantages of this technique are that (i) it is relatively quick, easy, and inexpensive to set up, (ii) it is a static method (the interfacial area is not changing as the measurement occurs (see Section 1)), and (iii) although most commonly used for liquid/vapour surface tension measurements, it can also be used to measure liquid/liquid interfacial tensions. The disadvantages are that (i) a relatively large amount of the solution of interest is required, (ii) the results depend on a contact angle that is usually difficult to measure (and thus one usually must trust that it is equal to zero), and (iii) for improved accuracy, theoretical corrections to the ideal case are needed.

3 THE WILHELMY PLATE METHOD

Another classic and popular technique for the measurement of equilibrium surface tensions is the Wilhelmy plate method. This technique involves dipping a thin plate into a liquid and directly measuring the force on the plate normal to the interface. Two different approaches can be used, i.e. the plate can be left suspended, bridging the two phases, or the plate can be pulled through the interface. The former case is often used in monolayer studies with a Langmuir trough, where surface tension changes can be monitored over time, due to changes in the surface coverage and packing of surface-active molecules. Such experiments can often run for hours. In the latter case, the plate is put in contact with the interface, and is then pulled out again, which is a common technique to measure the static surface tension of liquids (for air-liquid interfaces), or for the measurement of interfacial tension (for liquid-liquid interfaces). In practice, a wire attached to a scale or balance usually suspends the plate. The solution of interest is raised so that its surface just touches the bottom of the plate (see Figure 11.2). The increase in force measured by the balance, F, can be related to the surface tension as follows:

where P is the perimeter of the plate (approximately twice its length for a thin plate). As with the capillary rise method, the contact angle is usually difficult to measure. Often the plate is made of glass or platinum, which will be fully wetted (0 = О) if thoroughly cleaned. In this case equation (11.4) reduces to simply у = F/P. Surface roughness is often "added" to the plate to ensure complete wetting. Practically, though, the contact angle is never measured, but the surface tension-force relationship is calibrated by the prior measurement of known pure liquids (water).

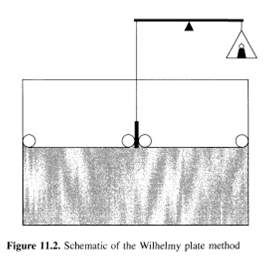
With the use of a modern electro-balance, very precise surface tension measurements can be obtained without the use of any theoretical corrections. This fact, along with the fact that this is a static measurement technique, makes the plate method a popular choice for precise equilibrium surface tension measurements. Note also that instrumentation which makes use of this method is readily available commercially. The disadvantages of this method are that a relatively large amount of liquid is needed.

4 THE DU NOUY RING METHOD

In this method, a thin wire ring is inserted below the interface (which can be either a liquid-vapour or liquid-liquid interface) and held horizontal. It is then pulled up through the interface and the force required to detach it from the interface, F, is measured by a balance. The surface tension is then given by the following:

where R is the radius of the ring. Note that for equation (11.5) to hold, the radius of the wire must be much smaller than the radius of the ring and that the solution must wet the wire (thus, a clean platinum wire is usually used).

This method is similar to the plate method described above, with a notable difference being the fact that it is not truly a static method. That is, the force measurement occurs while the wire ring is moving, and thus the interfacial area is increasing throughout the process. By performing the process in a slow enough fashion, a good approximation to the equilibrium surface tension can be obtained. However, this is often difficult to achieve, particularly for dilute solutions of highly surface-active materials that may require a relatively large amount of time to reach equilibrium. In addition, for precise measurements, the use of a correction factor, /, to the ideal case is required, i.e. the surface tension can be written as у = f y_Obs, where y_Obs is the observed surface tension obtained from equation (11.5). The correction factor is often given by the manufacturer of the tensiometer or can be found by using the tables given by Harkins and Jordan (3), who have tabulated this parameter as a function of R/r and R3/V, where r is the radius of the wire and (V= F/(gΔρ)) is the volume of the liquid raised above the free surface. The practical measurements are similar to those of the Wilhelmy plate technique, where the surface tension-force relationship is calibrated by prior measurements with known pure liquids.

In summary, the advantages of this technique are that (i) it is a classic technique for which systems are commercially available, and (ii) it can be used for liquid/vapour and liquid/liquid interfaces. The disadvantages are that (i) it is not a static technique, (ii) correction factors are usually required, (iii) a near zero contact angle (which is difficult to observe) is essential, and (iv) a relatively large amount of the solution of interest is required.

5 THE DROP WEIGHT METHOD

Another classical method of surface tension measurement is the drop weight method, where a drop is formed and then expelled from the tip of a vertical tube by slowly pumping the liquid through the tube, as shown in Figure 11.3. Initially, when the drop is relatively small, surface tension forces hold it to the tube. As more liquid is added, the drop grows. Eventually, the weight of the drop surpasses the surface tension forces and the drop falls. By measuring the weight of the drop, one can obtain this detachment force. In the ideal limit (discussed below), the surface tension can then be calculated from the following expression:

where W is the weight of the drop and r is the outer radius of the tube (if the liquid wets the tube material) or the inner radius (if the liquid does not wet the tube). In practice, to improve the accuracy, one usually measures the combined weight of several drops and then W is given by the total weight divided by the number of drops. This method can also be used to measure interfacial tensions by immersing the tip in another liquid. In this case, the volume of the drop, V, is usually measured, with the weight being given by ΔρgV. Note that as with the ring method described above, this technique is not a static measurement, as the interfacial area is increasing as the drop is formed. An approximation to the true equilibrium is obtained only if the drop is formed at a sufficiently slow rate.

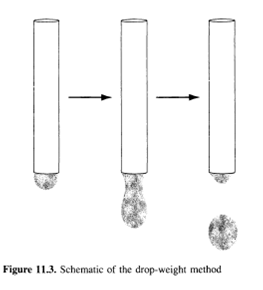
For precise measurements, the use of a correction factor is extremely important when using this method. That is, the surface tension can be written as у = у_оbs/f where y_obs is the observed surface tension obtained from equation 11.6 and / is a correction factor (defined in this manner so that f < 1). The need for this correction factor arises from the fact that a portion of the liquid contained in the drop remains attached to the tube when the drop detaches itself (as shown schematically in Figure 11.3), and thus the measured drop weight is less than the actual drop weight. Values of this correction factor have been empirically tabulated as a function of r/ V^1/3 by Harkins and Brown (4), as well as Lando and Oakley (5).

In summary, the advantages of this technique are that (i) it is relatively quick, easy, and inexpensive to set up, (ii) a relatively small amount of material is needed, (iii) the results do not depend on a difficult-to-measure contact angle, and (iv) it can be used to measure both liquid/vapour and liquid/liquid interfacial tensions. The disadvantages are that (i) an important correction factor is needed for accurate results, and (ii) the method is not a static one.

6 PENDANT/SESSILE DROP AND BUBBLE METHODS

A number of surface or interfacial tension measurement techniques rely on the geometric analysis of the interface formed by a drop or bubble. This analysis can be performed on a drop of liquid surrounded by a vapour (or less dense liquid), or a bubble of vapour (or less dense liquid) surrounded by a more dense liquid. The drop or bubble can take either a pendant (hanging) or sessile geometry form (see Figure 11.4). To simplify the analysis, axial symmetry is highly desired. This is easily accomplished in the pendant geometry case by the use of a circular, horizontal tip. It is more difficult to obtain in the sessile geometry situation, but can be accomplished primarily by using a smooth, flat and thoroughly cleaned solid surface. The drop or bubble is then photographed and digitized to obtain the profile of the interface. Note that only a two-dimensional image is required since the drop or bubble is cylindrically symmetric.

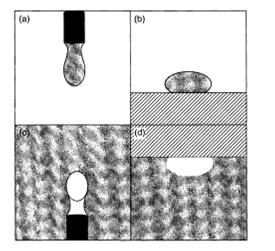
Figure 11.4. Schematics of the various shape methods: (a) the pendant drop method; (b) the sessile drop method; (c) the pendant bubble method; (d) the sessile bubble method. In all cases, the shaded areas represent the denser fluids, while the white areas represent air (in the case of liquid-air interfaces) or the less dense fluid (in the case of liquid-liquid interfaces)

The key to all shape techniques is that a balance between the counteracting forces dictates the shape or profile of the interface, i.e. (i) surface forces, which drive towards a perfectly spherical shape, and (ii) gravity, which drives towards a more (in the pendant geometry) or less (in the sessile geometry) elongated shape. An important parameter in these techniques is the Bond number, B, which represents the ratio of body forces (in this case gravitational) to surface forces, defined by the following:

where r is the length scale of the drop or bubble (often taken to be the radius of curvature at the drop or bubble apex). Typically, a bond number near unity is desired since these techniques rely on competition between body and surface forces.

For a given value of B, one can predict the shape of the interface by solving the Young-Laplace equation in differential form (where the boundary conditions are specific to each geometry). One can then determine the surface or interfacial tension, y, by finding the value of В which best matches the measured profile and by directly measuring r. A number of simplified, approximate technique were developed that do not require the entire profile to be matched. However, these approximations are less practical now that high-speed computers can be used to efficiently solve for the profile (see for example, Rotenberg et al. (6) and Cheng and Neuman (7)). This technique has become quite popular in recent years with the advent of inexpensive digital cameras for the acquisition of the interfacial profile, thus providing the data needed for the numerical analysis of the Young-Laplace equation. Several commercially produced tensiometers are available which use this technique.

There are various significant advantages for using this techniques. It is truly a static technique in that once equilibrium is reached, the interfacial area does not change. In particular, it is easy to control evaporation with these methods, so that one can study solutions which take a very long time to reach equilibrium, or volatile solutions (for example, aqueous solutions at a temperature near 100°C). For the drop methods, only a very small amount of liquid is needed, i.e. just enough to form one drop. However, as discussed above, for dilute solutions of highly surface-active materials, the depletion of the bulk solution concentration due to interfacial adsorption may be a problem and therefore, in such cases, the bubble methods, with a relatively large reservoir of liquid, are preferred. For pendant drops or bubbles, the results do not necessarily depend on a contact angle. For sessile drops or bubbles, a contact angle can be used as a boundary condition to the Young-Laplace equation, but this can easily be obtained from the imaged profile. Alternatively, one can analyze only the profile above (for the sessile drop) or below (for the sessile bubble) the equatorial plane and thus avoid the region of contact between the interface and the solid. Finally, these techniques can be used for both liquid/vapour and liquid/liquid interfacial tensions. The primary disadvantage to these techniques is that they are more difficult to set up compared to the other methods. However, this disadvantage is somewhat diminished now that commercial instruments are readily available.

7 THE SPINNING DROP METHOD

A different shape method to the ones described above is the spinning drop method, used for the measurement of ultra-low interfacial tensions. Here, two immiscible liquids are placed in a vessel, which is rotated, as shown in Figure 11.5. The centrifugal force resulting from the rotation causes the less dense liquid to collect at the center and form the "drop". As in the previous shape methods, there is a balance of forces, but here the interfacial forces balance the centrifugal force. As with the other shape methods described in Section 6, an image of the interface is taken and the Young-Laplace equation is used to determine the interfacial tension, which provides the best match between the theoretical and measured profile. For nearly cylindrical drops, the following approximate expression is often used:

where r is the radius of the drop and ω is the rotation rate. Practically, the ratio of the elongated length to the width of the drop as a function of rotation speed is correlated to the surface tension.

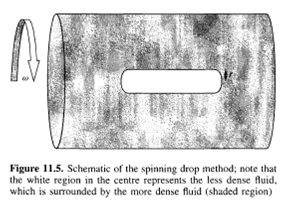
The primary advantage of this method over the other shape techniques given in Section 6 is that for pendant or sessile drops or bubbles of a given size, the gravitational force cannot be adjusted, whereas for a spinning drop the centrifugal force can be adjusted by varying the rotational frequency. As a result, this technique can be used to measure extremely low interfacial tensions (as low as 0.001 dyne/cm). In order to measure these extremely low interfacial tensions with the techniques described in Section 6, one would have to use an extremely small bubble or drop size to maintain a balance between body and surface forces. However, there is a practical limit to the size of a bubble that can be photographed and thus there is a practical limit to the values of the interfacial tensions that can be measured in this way. For the spinning drop method, the ability to vary the body force overcomes this limitation.

In theory, liquid/vapour measurements can be made by using this approach, where a vapour bubble replaces the less dense liquid drop. However, this would be rarely done for such measurements due to the difficulty of implementation, as discussed below. As with the other shape techniques described above, this is a static measurement and only small amounts of the liquids of interest are required. The primary disadvantage to this technique is that it is very difficult to set up and perform. Thus, this approach is usually only used to make measurements of extremely low interfacial tensions, where it would be the only reliable method available.

8 THE MAXIMUM BUBBLE PRESSURE METHOD

Although more often used to measure dynamic surface tensions (and thus is discussed in more detail in the following chapter), the maximum bubble pressure method can also be used to measure equilibrium surface tensions. With this technique, a tube or needle is immersed in the liquid and bubbles of vapour are continuously blown through it. If a needle with a small enough radius is used, such that the Bond number is much less than unity, the bubble will be approximately spherical and the radius of curvature will be at a minimum exactly when the bubble is a hemisphere of radius r (where r is the inner radius of the needle if the solution wets the needle, or the outer radius if it does not). By using the Young-Laplace equation, one can then determine

that the pressure will be at a maximum at this point, and the surface tension is thus given by the following expression:

where ΔР = P_bubble - (P_Air + Δρgh) (h is the depth to which the needle is submerged). Correction factors have been introduced, particularly to account from the deviations from spherical geometry caused by gravity/ buoyancy (see the following chapter). As with some of the detachment force methods, this is not truly a static measurement and thus equilibrium is only approximated by blowing the bubbles through at a slow enough rate. Again, as a practical matter, the ratio between the surface tension and the voltage given by the bubble pressure transducer is calibrated for a pure liquid (which will have no dynamic aspect to its surface tension). A two point calibration with two known liquids is often sufficient for accurate measurements of surfactant-containing solutions.

The advantages of this method include the following: (i) it is relatively easy and inexpensive to set up (and commercial systems are available), thanks to the advent of inexpensive electronic pressure transducers: (ii) it can be used in extreme environments, such as to measure the surface tension of molten metals, where it would be difficult to image the bubble interface, needed for use in the shape methods and where it would also be difficult to obtain a plate, ring or capillary tube made of suitable materials; (iii) the results do not depend on a difficult-to-measure contact angle; (iv) a relatively small amount of material is needed; (v) in theory, this technique can be applied to liquid/liquid interfaces. The main disadvantage to this technique is that it is not truly a static measurement, as discussed above in Section 1.

9 CONCLUSIONS

As can be seen from this brief review, the measurement of static surface tension is a well-established area, and there are many techniques available for this purpose. As a practical matter, many commercial instruments are now available for carrying out such measurements. In addition, several of the techniques can also be performed in the laboratory without resort to the use of any specialized instrumentation.

10 REFERENCES

1. Lord Rayleigh, О. М., On the theory of the capillary tube, Proc. R. Soc. London, A, 92, 184-195 (1915).

2. Lane, J. E., Correction terms for calculating surface tension from capillary rise, J. Colloid Interface Sci., 42, 145-149 (1973).

3. Harkins, W. D. and Jordan, H. F., A method for the determination of surface and interfacial tension from the maximum pull on a ring, J. Am. Chem. Soc, 52, 1751-1772 (1930).

4. Harkins, W. D. and Brown, F. E., The determination of surface tension (free surface energy), and the weight of falling drops: the surface tension of water and benzene by the capillary height method, J. Am. Chem. Soc, 41, 499-524 (1919).

5. Lando, J. L. and Oakley, H. Т., Tabulated correction factors for the drop-weight-volume determination of surface and interfacial tensions, J. Colloid Interface ScL, 25, 526-530 (1967).

6. Rottenberg, Y., Boruvka, L. and Neuman, W., Determination of surface tension and contact angle from the shapes of axisymmetric fluid interfaces, J. Colloid Interface Set, 93, 169-183 (1983).

7. Cheng, P. and Neuman, A. W., Computational evaluation of axisymmetric drop shape analysis-profile (ADSA-P), Colloids Surf., 62, 297-305 (1992).